Markov chain Monte Carlo extensions of the Ising model

This project consists of simulation software and an accompanying report on Markov Chain Monte Carlo (MCMC) simulations of magnetic spin models (specifically extensions of the Ising model). The software was written in Python and grew over time to encompass several different MCMC simulations of increasing complexity. We worked from the Metropolis algorithm to variations on the Wolff algorithm and the 2D XY model - observing vortex/anti-vortex phenomena not dissimilar to that featured in the work leading to the 2016 Nobel Prize in Physics: https://www.nobelprize.org/prizes/physics/2016/summary/.

In the 2D XY model there are excitations with nontrivial topology - vortices and anti-vortices (marked by blue and red circles below). These manifest when the angles of the surrounding spins sum to ±2π. The 2D XY model is the dual of the 2D Coulomb model; therefore, the two types of vortex correspond to electrical point charges with opposite signs. As with electrical charges, vortex and anti-vortex generally attract each other and annihilate. Furthermore, they only appear in pairs in our simulations due to periodic boundary conditions, analogous to pair production of an electron and positron in physics.

The finished simulation and data analysis software involved various features such as a fast Fourier transform to calculate the correlation between spins and the bootstrap statistical binning for error determination.

See the project here and our final report here.

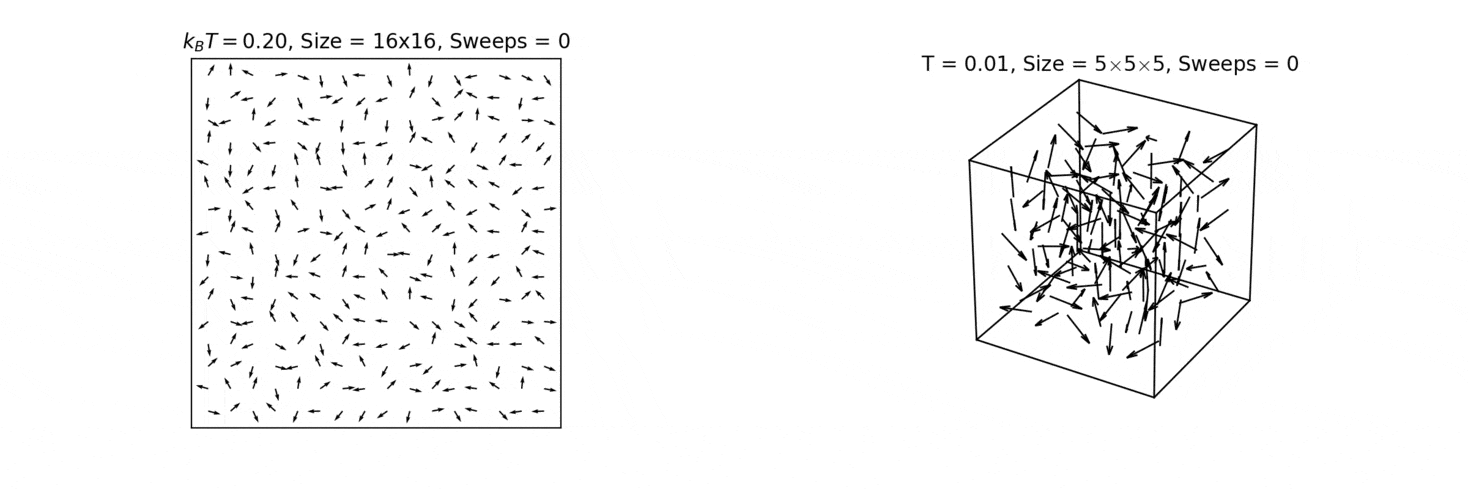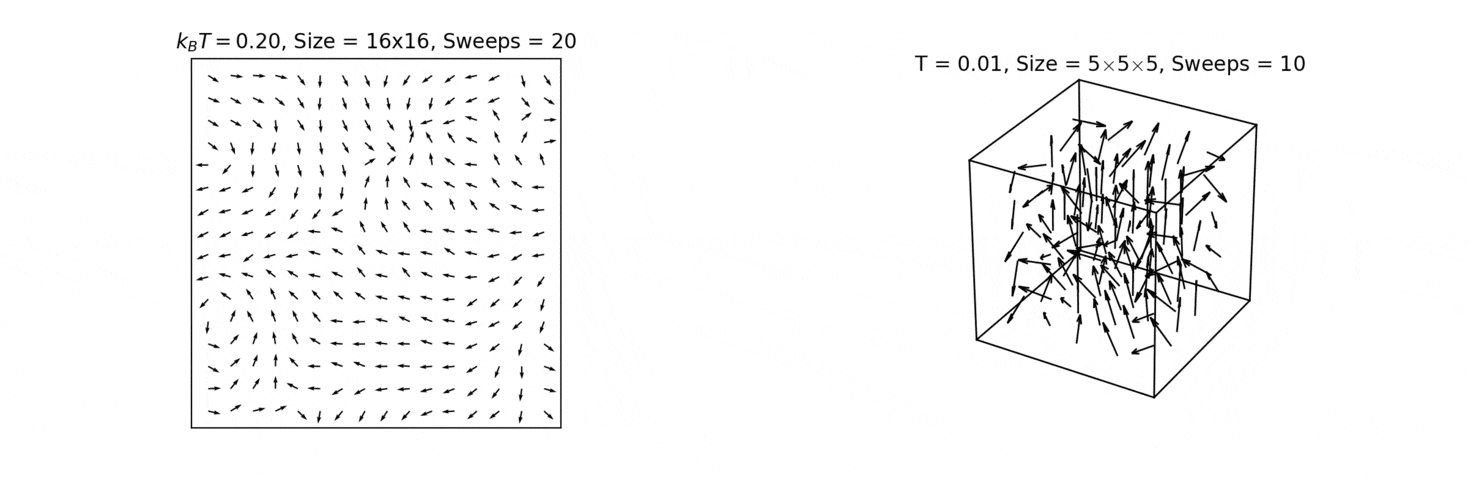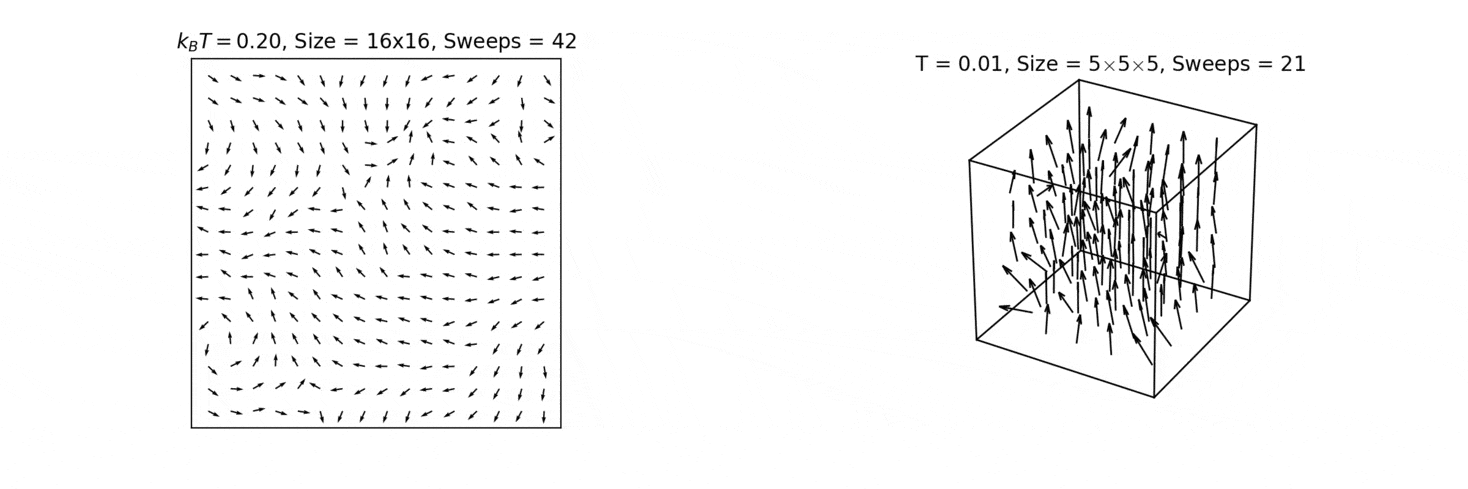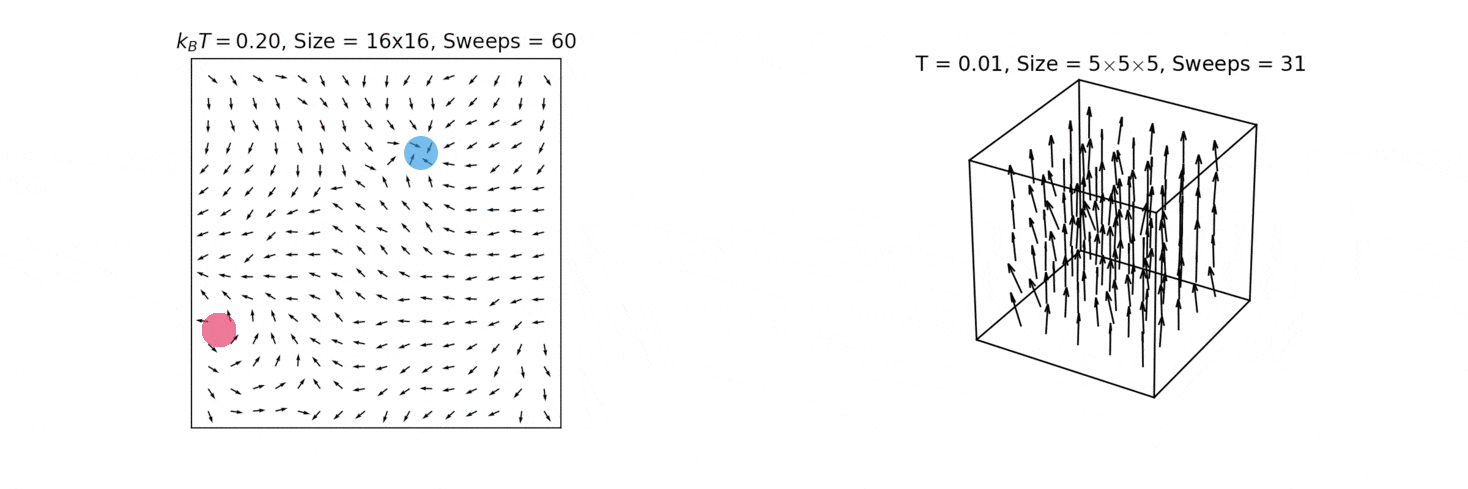
2D XY model, illustrating the formation of vortices (blue, where all spins point to the same point) and anti-vortices (red, where all spins point away from the same point), as well as the 3D Heisenberg model